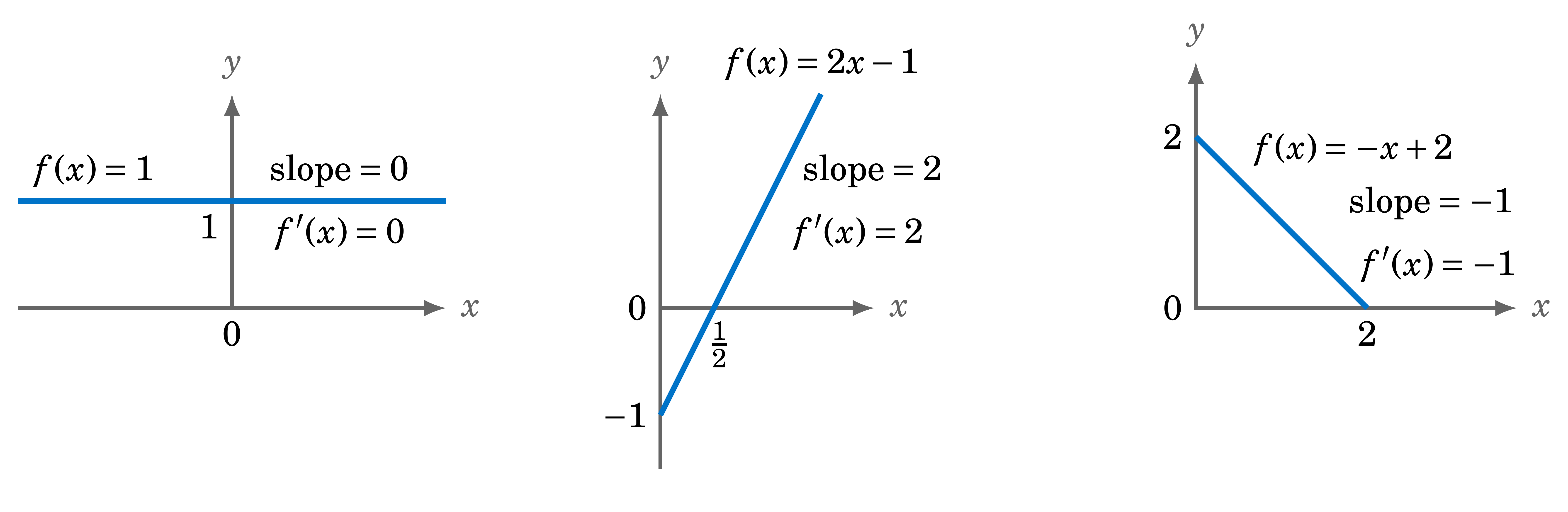The Derivative: Limit Approach ​

$$\text{Find the derivative of the function }f(x) = 1.$$
$$Solution:\text{ By definition, }f(x) = 1 \text{ for all } x, \text{ so: }$$
$$\begin{align*}
  f'(x) ~&=~ \lim_{\Delta x \to 0} ~\frac{f(x+\Delta x) ~-~ f(x)}
   {\Delta x}\\[6pt]
  &=~ \lim_{\Delta x \to 0} ~\frac{1 ~-~ 1}{\Delta x}\\[6pt]
  &=~ \lim_{\Delta x \to 0} ~\frac{0}{\Delta x}\\[6pt]
  &=~ \lim_{\Delta x \to 0} ~0\\[4pt]
  f'(x) ~&=~ 0
\end{align*}$$

$$\begin{exmp}\label{exmp:derivconst}
 Find the derivative of the function $f(x) = 1$.\vspace{1mm}
 \par\noindent\emph{Solution:} By definition, $f(x) = 1$ for all $x$, so:
 \begin{align*}
  f'(x) ~&=~ \lim_{\Delta x \to 0} ~\frac{f(x+\Delta x) ~-~ f(x)}
   {\Delta x}\\[6pt]
  &=~ \lim_{\Delta x \to 0} ~\frac{1 ~-~ 1}{\Delta x}\\[6pt]
  &=~ \lim_{\Delta x \to 0} ~\frac{0}{\Delta x}\\[6pt]
  &=~ \lim_{\Delta x \to 0} ~0\\[4pt]
  f'(x) ~&=~ 0
 \end{align*}
\end{exmp}$$